Fundamentals of Refrigeration: Combination Equations

In the real world, many situations will involve both the sensible heat equation and the latent heat equation.

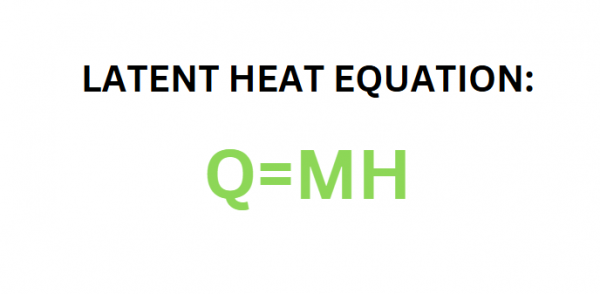
Example 1:

How many BTUs are required to change 5 pounds of 100ºF water into 212ºF steam?

Before solving this problem, it is essential to recognize that there are two distinct components. First, the temperature of the water must be raised from 100ºF to 212ºF, which involves sensible heat. Next, latent heat must be applied to facilitate the change of state from water to steam.  

The sensible heat equation is ‘Q’ equals ‘M’, ‘C’, ‘delta T’. The mass provided is 5 pounds. The problem states that water is being heated, and the specific heat of water is 1 BTU per pound degree Fahrenheit. The temperature change is 112ºF, which is the difference between the starting temperature of 100 degrees Fahrenheit and the final temperature of 212 degrees Fahrenheit. 

Once these values are plugged into the equation, it is found that 560 BTUs are required to raise the temperature of the water to the boiling point. However, this problem is not yet complete, as the water remains in a liquid state.

Now, examining the latent heat component, the latent heat equation is ‘Q’ equals ‘M’ multiplied by ‘h’. The mass remains at 5 pounds. Since water is still being considered, the latent heat of vaporization of water is known to be 970 BTUs per pound. By plugging these values into the equation, it is determined that 4,850 BTUs are required to change 5 pounds of 212ºF water into 212ºF steam.

The final answer is the sum of the sensible heat and latent heat, which equals 5,410 BTUs. It is notable that the latent heat required accounts for 90% of the total heat needed. This emphasizes that latent heat often dominates specific heat in situations involving a change of state.

Example 2:

How much heat must be removed from 2 pounds of 220ºF steam to make 10ºF ice?

This problem consists of five components. First, it is necessary to remove sensible heat from the steam to lower its temperature to the boiling point. Second, latent heat must be removed from the steam to change its state to water. Third, the water temperature must be lowered to the freezing point, which involves only sensible heat. Fourth, transitioning from water to ice requires latent heat. Fifth, sensible heat must again be removed from the ice to lower its temperature to 10ºF.

While this can seem intimidating, if broken down into its parts, no single step is too difficult. Let’s start with the sensible heat required to lower the temperature of the steam from 220ºF to 212ºF. The sensible heat equation is ‘Q’ equals ‘M’, ‘C’, ‘delta T’. The mass is given as 2 pounds. The problem states that steam is being cooled, so the specific heat of steam is 0.5 BTU per pound degree Fahrenheit. The temperature change is 8ºF, which is the difference between the starting temperature and the final temperature.

Once these values are plugged into the equation, it is found that 8 BTUs are required to lower the temperature of the steam to 212ºF.

To calculate the heat that must be removed to change from steam into water. The latent heat equation is ‘Q’ equals ‘M’ multiplied by ‘h’. The mass is still 2 pounds, and it is known that the latent heat of vaporization of water is 970 BTUs per pound. Once these values are plugged into the equation, it is found that 1,940 BTUs must be removed in this phase change.

Now it is necessary to calculate the sensible heat that must be removed to lower the water temperature from the boiling point, 212ºF, to the freezing point, 32ºF. The sensible heat equation will be used for this step. The mass is 2 pounds, and the specific heat of water is 1 BTU per pound degree Fahrenheit. The temperature change is 180ºF, which is the difference between 212ºF and 32ºF. Crunching the numbers, it is found that 360 BTUs are required to lower the temperature of the water to 32ºF.

The fourth step is to calculate the latent heat that must be removed to freeze the 2 pounds of water. Using the latent heat equation, 2 pounds of mass will be multiplied by the latent heat of fusion for water, which is 144 BTUs per pound. The heat that must be removed in this step is 288 BTUs.

The fifth step in this problem is to calculate the heat that must be removed to lower the temperature of the ice to 10ºF. The sensible heat equation will be utilized for the third time. The specific heat of ice is 0.5 BTUs per pound degree Fahrenheit, so the calculation involves multiplying the 2-pound mass by 0.5 BTUs per pound degree Fahrenheit by 22 degrees Fahrenheit. A total of 22 BTUs must be removed to lower the temperature of the ice.

As a final step, the sum of the five steps must be found. By doing this, it can be determined that 2,618 BTUs must be removed from 2 pounds of 220ºF steam to form 2 pounds of 10ºF ice.

It is worth noting that the latent heat required to condense the steam is the largest component of this problem, by far. 74% of the BTUs were removed in the phase change from steam to water.